【数学运算】
某人开车从A镇前往B镇,在前一半路程中,以每小时10公里的速度前进;而在后一半的路程中,以每小时15公里的速度前进。则此人从A镇到达B镇的平均速度是每小时多少公里?
A. 12
B. 12.5
C. 14
D. 14.5

本题考查行程问题,求等距离平均速度。
解法1:利用公式求解。前后半路程相同,根据“等距离平均速度公式”可得:V=2V1V2/(V1+V2)=2*10*15/(10+15)=12。故答案为A。
解法2:利用假设法求解。根据两个速度可设路程为150公里,那么,前半段用时:150/10=15小时,后半段用时:150/15=10小时。根据“平均速度=总路程/总时间”可知:V=(150+150)/(15+10)=12公里/小时。答案为A。
【知识拓展】
1. 平均速度的核心公式:平均速度=总路程÷总时间。
2. 【等时间平均速度】
已知:某人走完全程的前一半时间,速度为V1;后一半时间,速度变为V2。求整个全程的平均速度。
第1步,设总路程为S,前一半时间为t1,后一半时间为t2,t1=t2=t。全程平均速度=总路程÷总时间=S÷(t1+t2)。
第2步,S1=v1×t1;S2=v2×t2。
第3步,S=S1+S2=v1×t1 + v2×t2=v1×t+v2×t=(v1+v2)×t
第4步,全程平均速度=S÷(t1+t2)=(v1+v2)×t÷(t+t)=(v1+v2)÷2
归纳:已知在相同时间内的不同速度,求平均速度的这一类平均速度称为:等时间平均速度。等时间平均速度=(v1+v2)÷2。
(也许,此刻,你觉得这4步太麻烦了,心里正默默地吐槽:不看这么枯燥地推导过程,我也知道“平均速度=速度之和÷2”…………
是否真的每次都能如此呢?
请看下一条,你就会知道上一题你为什么选错了……
你也就能明白为什么一定要理解如此枯燥地推导过程!!!)
3. 【等距离平均速度】
已知:某人走全程的前一半路程,速度为V1;后一半路程,速度变为V2。求整个全程的平均速度。
第1步:设总路程为2S,前一半时间为t1,后一半时间为t2。全程平均速度=总路程÷总时间=2S÷(t1+t2)。
第2步:t1=S÷v1;t2=S÷v2
第3步:
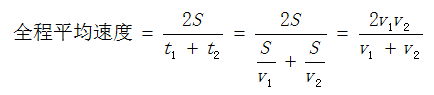
(明显,此时,平均速度≠速度和÷2)
第4步:从第3步可知,S的值并不影响平均速度的大小,因此,为了简化计算,为了不死记公式,可用“设1思想”。回顾整个思路,从一开始就将总路程赋值为v1和v2的公倍数, 如本题,设一半路程为10和15的公倍数150公里。因此,平均速度的公式变为:
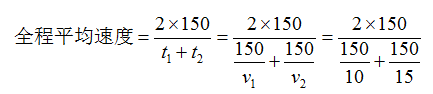
(该法称为“特值法”)
整个计算过程就变得简单明了,所以,用“特值法”求解【等距离平均速度】最快最好。
归纳:已知用不同速度走相同的路程,求整体的平均速度。这一类平均速度称为:等距离平均速度。等距离平均速度=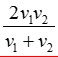 ,或用“特值法”。
,或用“特值法”。
编辑:中政行测
上一篇:行测答题技巧:精讲行程问题
下一篇:行测答题技巧:行程求平均速度