第三部分 数量关系 在这部分试题中，每道题呈现一段表述数字关系的文字。要求你迅速、准确地计算出答案。备考阶段推荐使用步知公考名师大咖课程(花木君/风暴羚羊)复习备考。
51 甲、乙两人从环形跑道的 A 点同时出发背向而行，6 分钟后两人第一次相遇，相遇后两 人的速度各增加 10 米每分钟，5 分钟后两人第二次相遇，问环形跑道的长度为多少米?
A.600
B.500
C.400
D.300
【答案】 A
【解析】本题为行程问题中的相遇问题，根据路程和=速度×相遇时间可得，s=(v 甲+v 乙)×6，s=(v 甲+v 乙+20)×5，解得 s=600，故本题答案选 A。
52 四个士烧杯甲、乙、丙、丁的容量比为 3∶4∶8∶10。用甲烧杯装满与水比重相同的 A 溶液倒入丙烧杯后，用水兑满，然后将混合的溶液例入乙烧杯至满后，将剩下的部分倒入丁 烧杯并用水将丁烧杯注满，问此时乙烧杯中 A 溶液的浓度是丁烧杯中的多少倍?
A.2
B.2.5
C.4
D.6
【答案】 B
【解析】
53 车间共有 50 名工人，年底进行考核，有 12 人业务能力为优，10 人政治表现为优，没有 一项考核成绩为优的有 34 人，车间要向上级单位推荐 2 名两项考核均为优的工人作为先进 个人的候选人，问有多少种推荐方案?
A.12
B.15
C.18
D.21
【答案】 B
【解析】
54 甲、乙两个小分队的人数之和在 90 到 110 之间，如果从甲队调一定人数给乙队，则乙队 的人数就是甲队的 2 倍;如果乙队调同样的人数给甲队，则甲队的人数就是乙队的 3 倍。问 甲队调多少人给乙队之后，乙队的人数是甲队的 5 倍?
A.18
B.24
C.30
D.36
【答案】 D
【解析
】
55 箱子里有标号 1 至 10 共 10 个球，小张随机取了三个球并记下号码后将球放回，小李也 随机取了三个并记下号码。这时发现两人取的球的号数之积都恰好是 144。已知小张的号数 之和比小季的大，那么小张取的球的号数之和是多少?
A.19
B.17
C.16
D.14
【答案】 A
【解析】
56 车间里要加工的手套副数是口罩个数的 2 倍，如果每位工人加工 3 个口罩，则还需额外生产 2 个口罩：如果每位工人加工 7 副手套，则会超额完成 6 副手套。如每位工人每 5 分钟 可生产 1 副手套或 1 个口罩，且车同内的工人数减少一半，问至少需要多少分钟才能完成全 部生产任务?
A.85
B.90
C.95
D.100
【答案】 D
【解析】设 x 人，则有 2(3x+2)=(7x-6)，解得 x=10，故手套有 32 副，口罩有 64 个，总共有 96 个，分给 5 个人，每个人分得 19 个，需要 19×5=95 分钟，还剩下 1 个，需要 5 分钟， 所以共需 100 分钟。因此，本题答案选 D 项。
57 工地仓库里有水泥若干，第一天用掉了前一天剩余库存的 1/3 后又补充了 500 袋，第二天 用掉了第一天剩余库存的 1/9 后又补充了 400 袋，此时仓库的水泥库存是原有水泥的 2 倍， 则仓库原有水泥多少袋?
A.480
B.540
C.600
D.660
【答案】 C
【解析】根据题意，将选项代入，排除，即可得到答案。
58 甲、乙两名实力相当(印每一局两人中任意一人获胜的概宰相同)的棋手进行 7 局 4 胜制的 比赛，前 3 局赛完后，甲以 2：1 领先于乙，那么甲获得最后胜利的概串是多少?
A.2/3 B.3/4 C.5/8 D.11/16
【答案】 D
【解析】甲获胜的情况是在第四、第五、第六、第七这四局中，赢两局 则有以下情况：
共打七局：第七局胜，第四五六局中胜一场，概率为3/16
共打六局：第六局胜，第四五局胜一场，概率为 2/8
共打五局：第四局和第五局均胜，概率为 1/4
则胜利的概率为 11/16
59 有一批规格为 1 吨的铜锭，计划安排用 8 辆载重 9 吨的汽车运送，要求不得对钢锭进行 切割，预计每辆车运送 25 次正好运完。每辆车运送了 13 次之后，甲方要求增派若干辆载重 24 吨的汽车，以能够一次将剩下的钢锭全部运完，问需要增派多少辆汽车?
A.33
B.34
C.35
D.36
【答案】 A
【解析】根据题意，总共有的钢锭为 8*9*25=1800,后来每辆车运送了 13 次，共运送了 13*8*9=936，那么还余下了 1800-936=864，要想一次运送完，设需要 x 辆车，则 24x+8*9=864, 则 x=33
60 论文集中收录了一篇十乡页的论文，其所在各项的所有页码之和为 1023，问这篇论文之 后的一篇论文是从第几页开始的?
A.94
B.99
C.102
D.109
【答案】 B
【解析】
页码是公差为 1 的等差数列，页码之和为 1023，根据等差数列求和公式：前 n 项和=中位数
×项数，并且根据论文十多页这一条件，从项数 11 开始代入。
假如项数为 11，则 1023/11=93，即第 6 项为 93，第 11 项为 98，符合题意，后一篇论文从 第 99 页开始。
61 小明买了 7 本书共花去 100 元，后发现有一本书质量有问题，故补了若干元换了另外一本书，回来后发现，退换后 7 本书的价格成等差数列且均为整数元，而最贵的书价格为 26元，问最便宜的书多少钱?
A.2 元
B.6 元
C.8 元
D.14 元
【答案】 C
【解析】 7 本书成等差数列且均为整数，且为 100 元以上
代入 A，最便宜书为 2 元，7 本书价格之和 14×7=98，不到 100 元，与条件矛盾，排除 代入 B，最便宜书为 6 元，由最贵书为 26 元可得，公差不为整数，与条件矛盾，排除
代入 C，最便宜书为 8 元，7 本书之和为 119，该等差数列为 8,11,14,17,20,23,26,119-100 多 补了 19 元，符合题意。
代入 D，最便宜书为 14 元，7 本书价格之和为 140，该等差数列为：14,16,18,20,22,24,26， 根据原来 7 本书 100 元，补了若干元换本书这个条件，可知换后的书比换之前贵，该数列不 符合题意，排除。
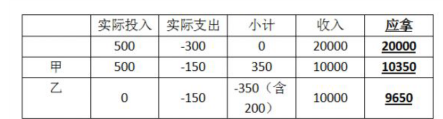
62 甲乙两人共同投资一件收藏品，约定好费用支出均分，利润也均分。某次甲给了乙 500 元用于支付专家鉴定费，结果专家只向乙收取了 300 元鉴定赞，但乙忘记将余下的钱给甲。 后收藏品以 20000 元的价格转手，问此时甲乙应该各拿走多少钱?
A.甲 10050 元，乙 9950 元
B.甲 10200 元，乙 9800 元
C.甲 10150 元，乙 9850 元
D.甲 10350 元，乙 9650 元
【答案】 D
【解析】
63 某旅游公司有能载 4 名乘客的轿车和能载 7 名乘客的面包车若干辆，某日该公司将所有车辆分成车辆数相等的两个车队运送两支旅行团。已知两支旅行团共有 79 人，且每支车队 都满载，问该公司轿车数量比面包车多多少辆?
A.5
B.6
C.7
D.8
【答案】 B
【解析】 设轿车 X 辆，面包车 Y 辆
根据题意可知 4X+7Y=79，由奇偶性可得，7Y 必为奇数;同时根据条件可将车辆分成相等 的两个车队，可知 X+Y 为偶数。
有以下情况：
Y=1，则 X=18，X+Y=19 为奇数，与条件矛盾，排除。
Y=3，则 X 不为整数，车辆不可能为小数，排除。
Y=5，则 X=11，5+11=16 为偶数，符合条件，该假设成立。 则 X-Y=6
64 编号为 1-50 的选手参加一个爬楼比赛，楼高为 60 层，所有选手在第 1 层均获得一个特 别的号牌，此后每经过一个楼层，如果选手的编号正好是楼层数的整数倍，就将得到一个特 别的号牌，所有选手都到达终点后，正好持有 3 个特别号牌的选手有多少人?
A.1
B.4
C.7
D.10
【答案】 B
【解析】 正好持有 3 个特别号牌，说明该选手的编号恰好是 2~60 中三个数的整数倍数 任意一个数是都有 1 和自身两个因数，则另外两个因数必须是相同的，即平方数因子 编号 4，是 1、2、4 层的整数倍
编号 9，是 1、3、9 层的整数倍 编号 25，是 1、5、25 层的整数倍 编号 49，是 1、7、49 层的整数倍 共 4 人。
65 晚上 21 点整，甲乙两车同时从 A 地出发匀速开往 B 地，同一时间丙丁两车从 B 地出发匀速开往 A 地，甲车时遽是乙车的 3 倍，乙车行驶 3 小时后首先与丙相遇，再行驶 1 小时
之后与丁相遇，若 4 辆车到达目的地的时闻正好都是第二天内的整点时同，问甲车和丙车是 在几点相遇的?
A.0 点整
B.23 点 30 分 C.23 点整 D.22 点 30 分
【答案】 C
精华推荐
编辑：行测
关于我们|业务合作|版权声明|站点地图| |营业执照 |出版物经营许可证
电子公告服务批文（湖南省）|电子公告服务批文（长沙市）|增值电信业务经营许可证：湘B2-20150109
湘公网安备 43012102000156号 湘ICP备13008748号-3 Copyright © 
All Rights Reserved.
