在一个正方形内画中、小两个正方形，使三个正方形具有公共顶点

　　题目：

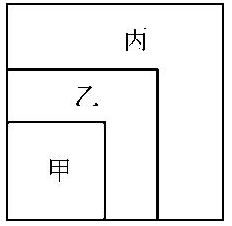
　　在一个正方形内画中、小两个正方形，使三个正方形具有公共顶点，这样大正方形被分割成了正方形区域甲，和L形区域乙、丙。已知三块区域甲、乙、丙的周长之比为4∶5∶7，并且区域丙的面积为48，求大正方形的面积( )。

　　A. 96

　　B. 98

　　C. 200

　　D. 102

　　解析：

　　由于乙和丙是“L型区域”为非规则图形，我们采用“平移”思想。乙的周长等于中正方形的周长，丙的周长等于大正方形的周长，由题干“甲、乙、丙的周长之比 为4∶5∶7”可得，小、中、大正方形的周长之比为4∶5∶7，则小、中、大正方形的面积之比为16:25:49。我们设大正方形面积为49a，则中正方 形为25a，从而得到丙的面积为49a-25a=24a，题目已知“区域丙的面积为48”，故24a=48得到a=2，则大正方形的面积为 49a=49×2=98，因此，本题答案为B。

　　点击查看更多行测真题