行测经典视频：数学运算之几何问题（1）

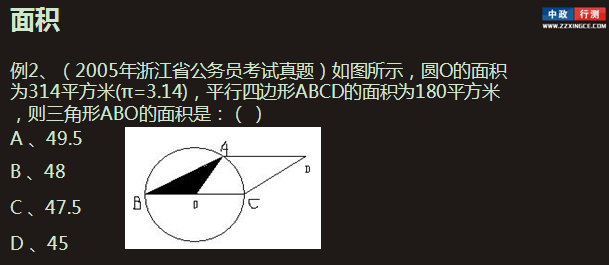
例题讲解：
    本题考查几何中圆和三角形面积。解法1：连接AC，显然AC平分平行四边形ABCD，所以，三角形ABC的面积=180/2=90。其中，三角形ABO和ACO等高等底，面积相同，那么，三角形ABO的面积=90/2=45。
    解法2：根据圆的面积是314平方米，求得圆的半径=10米，那么，平行四边形ABCD的底是10*2=20米，所以，它的高等于180/20=9米，从图中可以看出，三角形ABO与平行四边形同高，底等于半径，那么，它的面积=10*9/2=45。答案为D。
 
思路点拨：
    这道几何题并不难，就是考常用的面积公式，如果足够熟悉圆、平行四边形、三角形的面积公式，并找出它们之间的关联，比如三角形ABO的底等于圆的半径、平行四边形ABCD和三角形ABO等高，其面积是ABO的四倍等，找到了这些关联点，解题自然水到渠成。

想跟着老师一起学习？登陆注册中政行测在线备考平台