行测经典视频：数学运算之几何问题（2）

例题讲解：
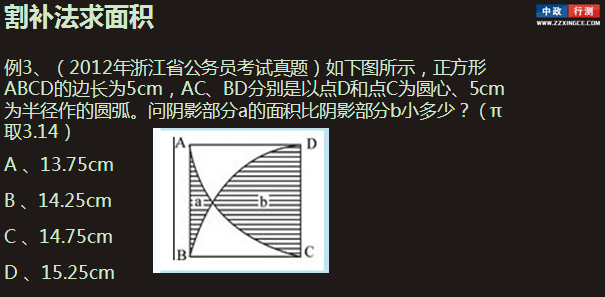
    本题考查几何问题。仔细观察图形会发现：两个空白部分面积相等，那么设每个空白部分的面积为c，看得出阴影部分b加上空白部分正好构成一个扇形，阴影部分a加上空白部分正好等于正方形面积减去扇形面积，即：b+c=1/4•πr^2，a+c=5^2-1/4•πr^2，两式相减可得：b-a=14.25cm。答案为B。
 
思路点拨：
    几何问题中求不规则图形的面积时，常用的一种思想就是“割补平移”：通过添加或移除部分使得图形变成可以利用公式求解面积的规则图形，然后加上或减去移动部分的面积，求出不规则图形的总面积。本题就可以利用割补平移思想解题，阴影部分b加上空白部分正好构成一个扇形，阴影部分a加上空白部分正好等于正方形面积减去扇形面积，两两相减，求出a和b的面积之差。

想跟着老师一起学习？登陆注册中政行测在线备考平台